【算法】字符串匹配KMP算法详解

之前在学数据结构的时候就没有太弄懂KMP算法，近日恰好刷到一道查找子串位置的算法题，所以好好复习一下KMP算法。

KMP算法是一个快速查找匹配子串的算法，它的作用是在原字符串中快速找到匹配字符串。KMP算法的复杂度为O(m+n)。

KMP算法之所以能够在O(m+n)的复杂度内完成查找，是因为它能够在非完全匹配的过程中提取到有效的信息进行复用，从而减少重复匹配的消耗。

过程演示

首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

img

因为B与A不匹配，所以搜索词往后移，知道字符串中有一个字符与搜索词的第一个字符相同为止。

img

接着比较字符串和搜索词的下一个字符，还是相同。

img

直到字符串有一个字符，与搜索词对应的字符不相同为止。

img

这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

img

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。

img

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

　移动位数 = 已匹配的字符数 - 对应的部分匹配值

因为 6 - 2 等于4，所以将搜索词向后移动4位。

img

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

img

因为空格与A不匹配，继续后移一位。

img

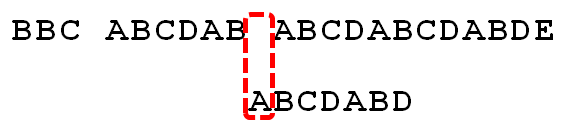
逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

img

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

img

这一块的部分如果用代码演示，就是下面这样：

//用haystack代表原字符串，needle代表匹配字符串
//next数组用来记录部分匹配表中的部分匹配值
int n=haystack.size();
int m=needle.size();

for(int i=0,j=0;i<m;i++)//用i来做原字符串中的指针，j来表示匹配字符串中的指针
{
	while(j&&haystack[j]!=needle[i])j=next[j-1];//对应公式　移动位数 = 已匹配的字符数 - 对应的部分匹配值
    if(needle[j]==haystack[i])j++;//如果找到相等的部分，指针向后移一位
    if(j==m)return i-m+1;//如果j指针已经移到匹配字符串末尾，则返回i-m+1即是匹配字符串的位置
}
return -1;//如果没找到匹配字符串就返回-1

那么如何求next数组（即部分匹配表）呢？

next数组求解

我们再仔细观察一下KMP的匹配过程：

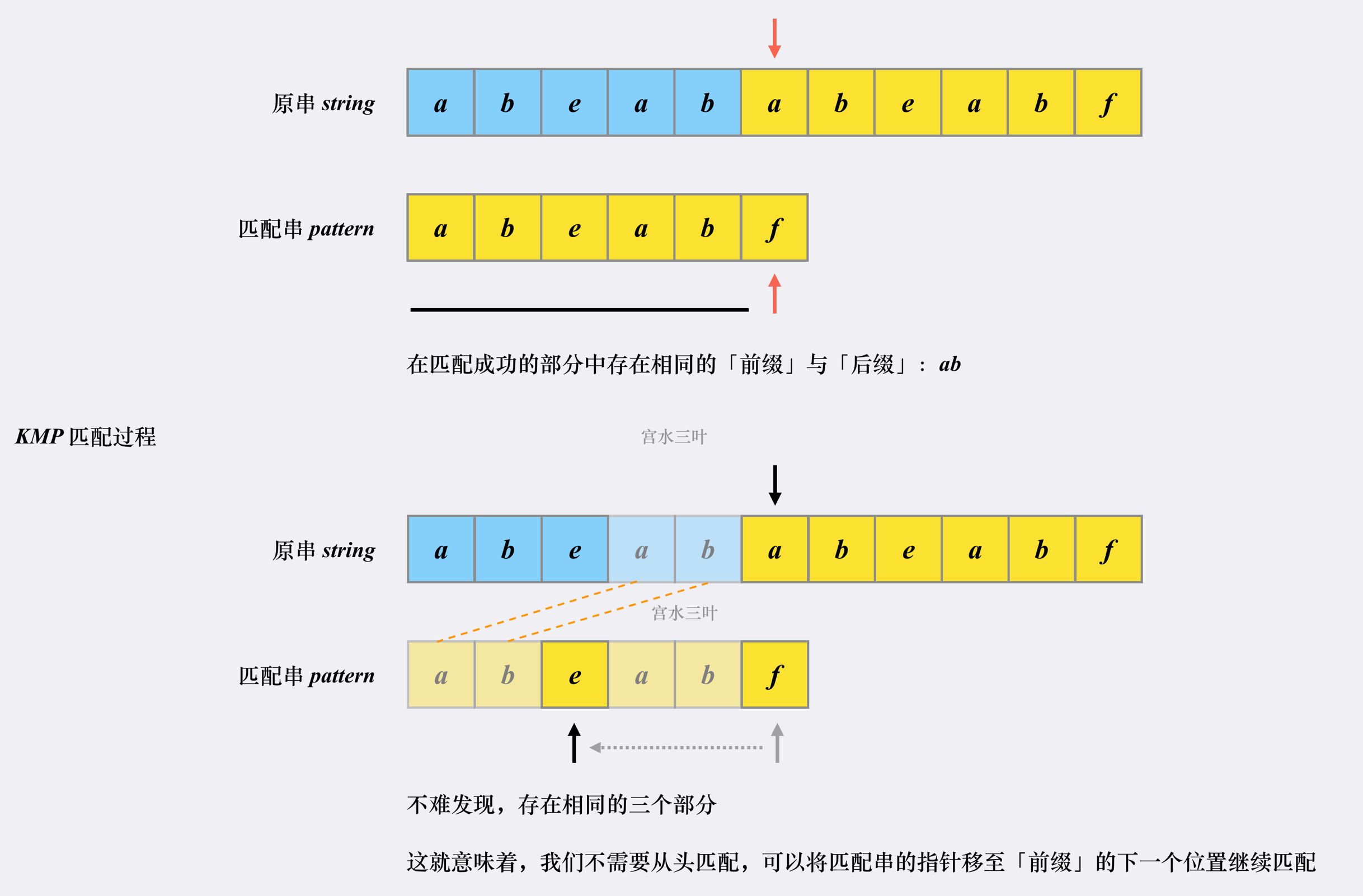
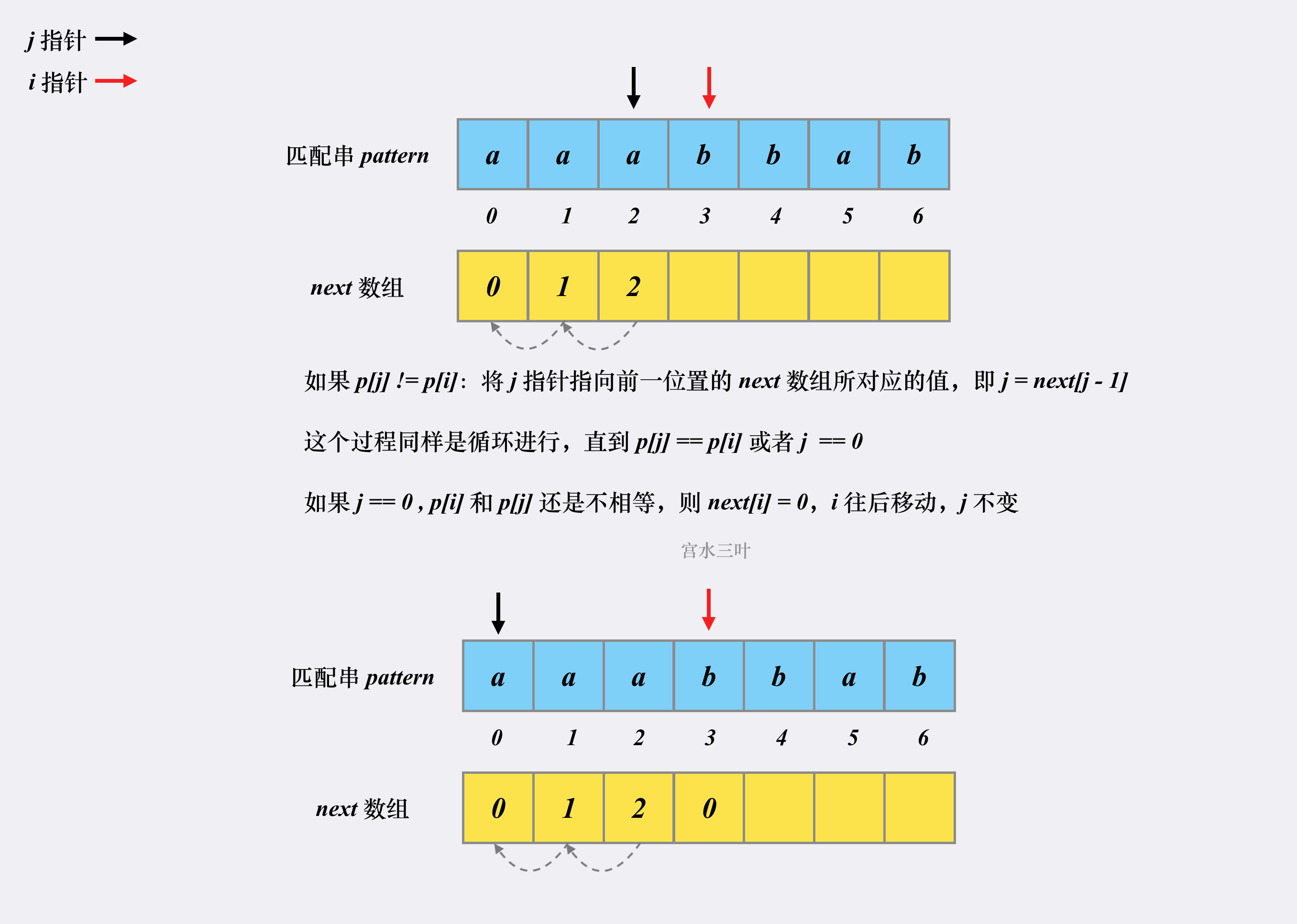
首先匹配串会检查之前已经匹配成功的部分中里是否存在相同的「前缀」和「后缀」。如果存在，则跳转到「前缀」的下一个位置继续往下匹配：

跳转到下一匹配位置后，尝试匹配，发现两个指针的字符对不上，并且此时匹配串指针前面不存在相同的「前缀」和「后缀」，这时候只能回到匹配串的起始位置重新开始：

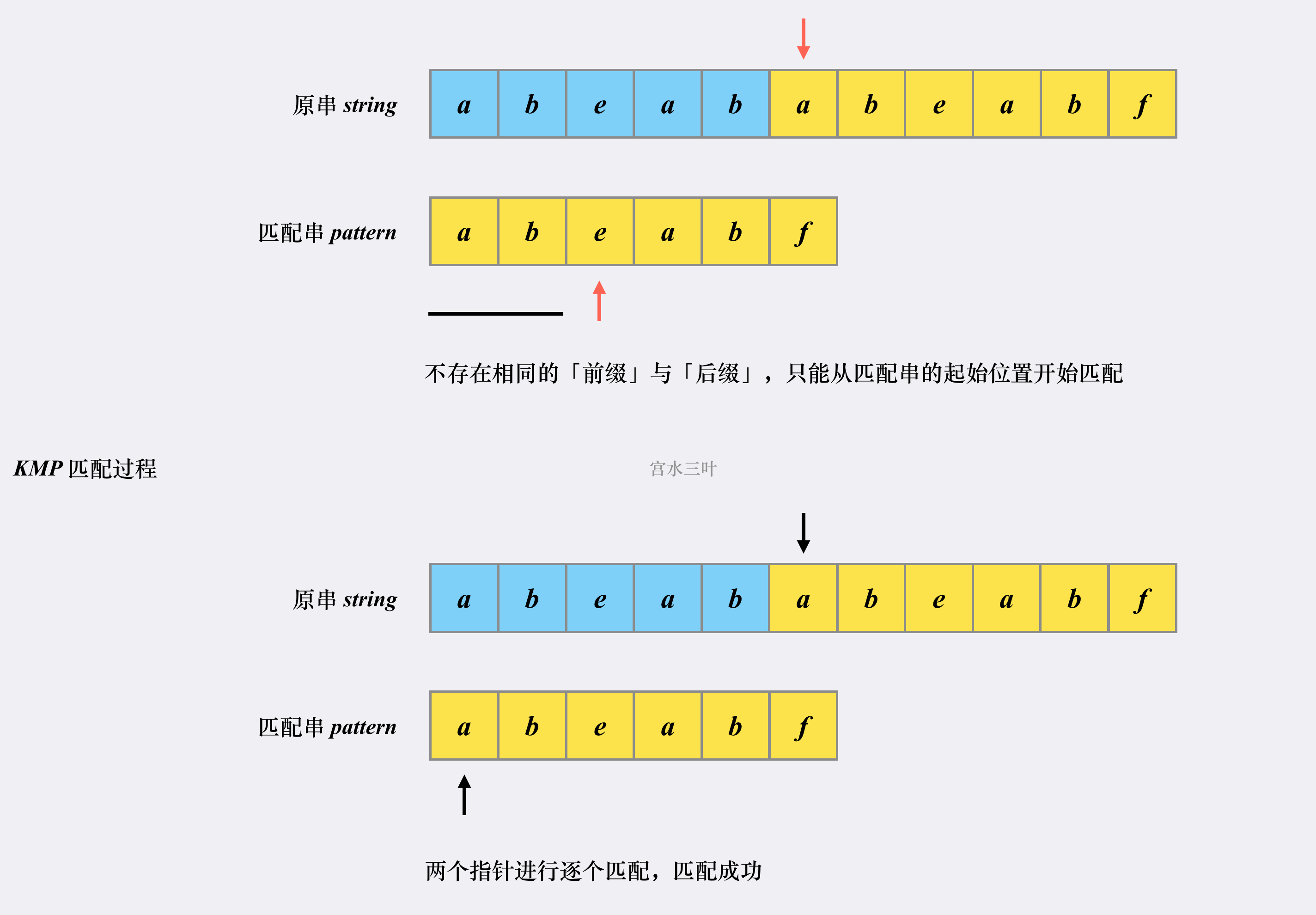
所以你发现了吗？从匹配串某个位置跳转下一个匹配位置这一过程是与原串无关的，我们将这一过程称为找 next 点。next数组中每个值的含义其实就是该下标应该跳转到的目标位置。

比如上图中的字符串abeabf对应的next数组应该是：

匹配串	a	b	e	a	b	f
匹配值	0	0	0	1	2	0

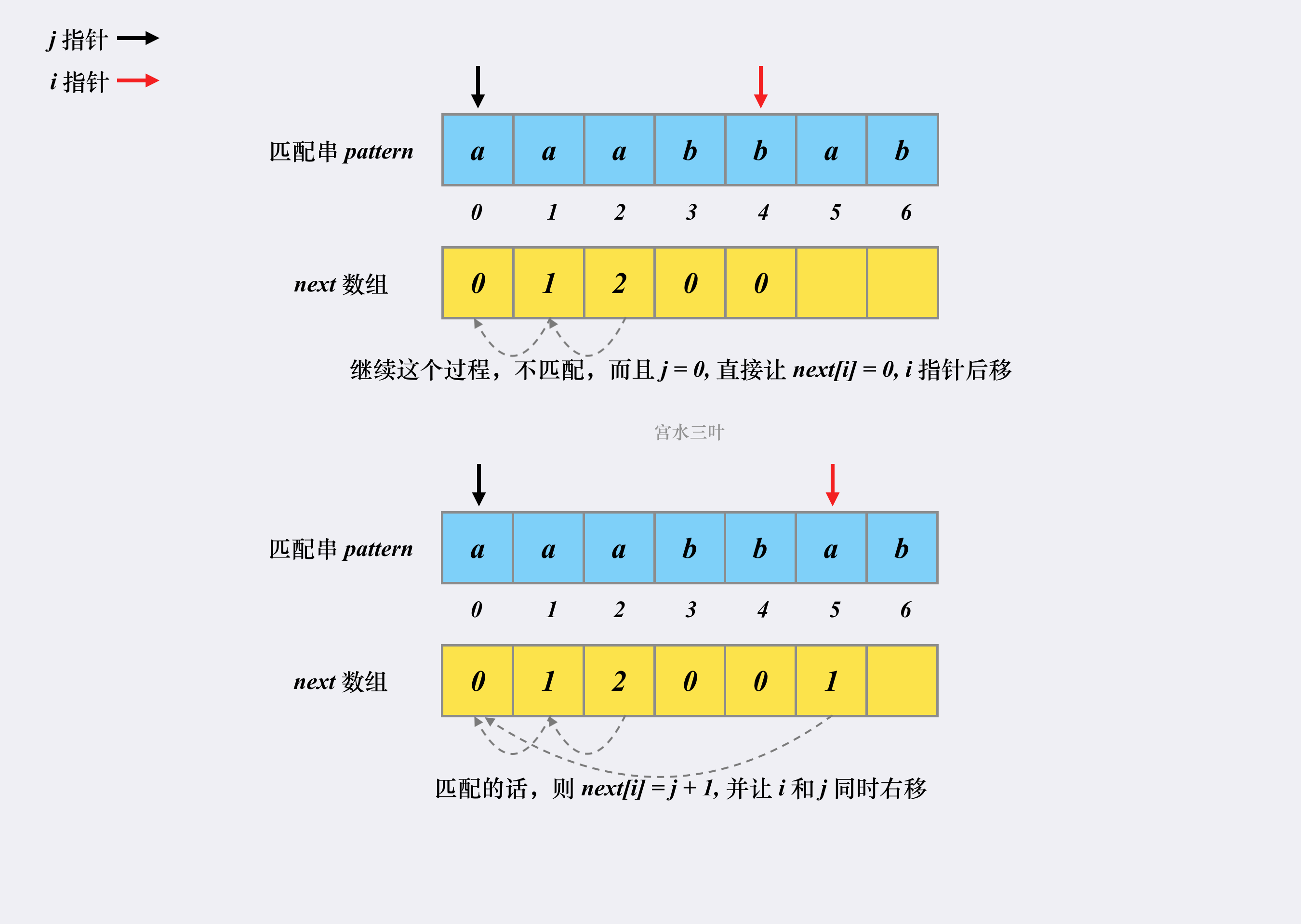
假设i指针指向原串string，j指针指向匹配串pattern，当i指针指向string[5]，即字母'a'，j指针指向pattern[5]，即字母'f'时，由于前五轮比较都是匹配的，因此pattern的指针j=j-(j-next[j-1])=next[j-1]=2，直接跳转到patter[2]，即字母'e'与string[5]进行比较。这是因为KMP的优化过程就是检查已匹配部分的相同前缀和后缀。

因此，next数组的构建过程也就是寻找匹配串pattern的相同前缀和后缀的过程，然后从第一个相同的后缀开始记匹配值为1，而后递增，直到找到第一个不匹配的后缀，再重新记为0。

3.png

4.png

5.png

6.png

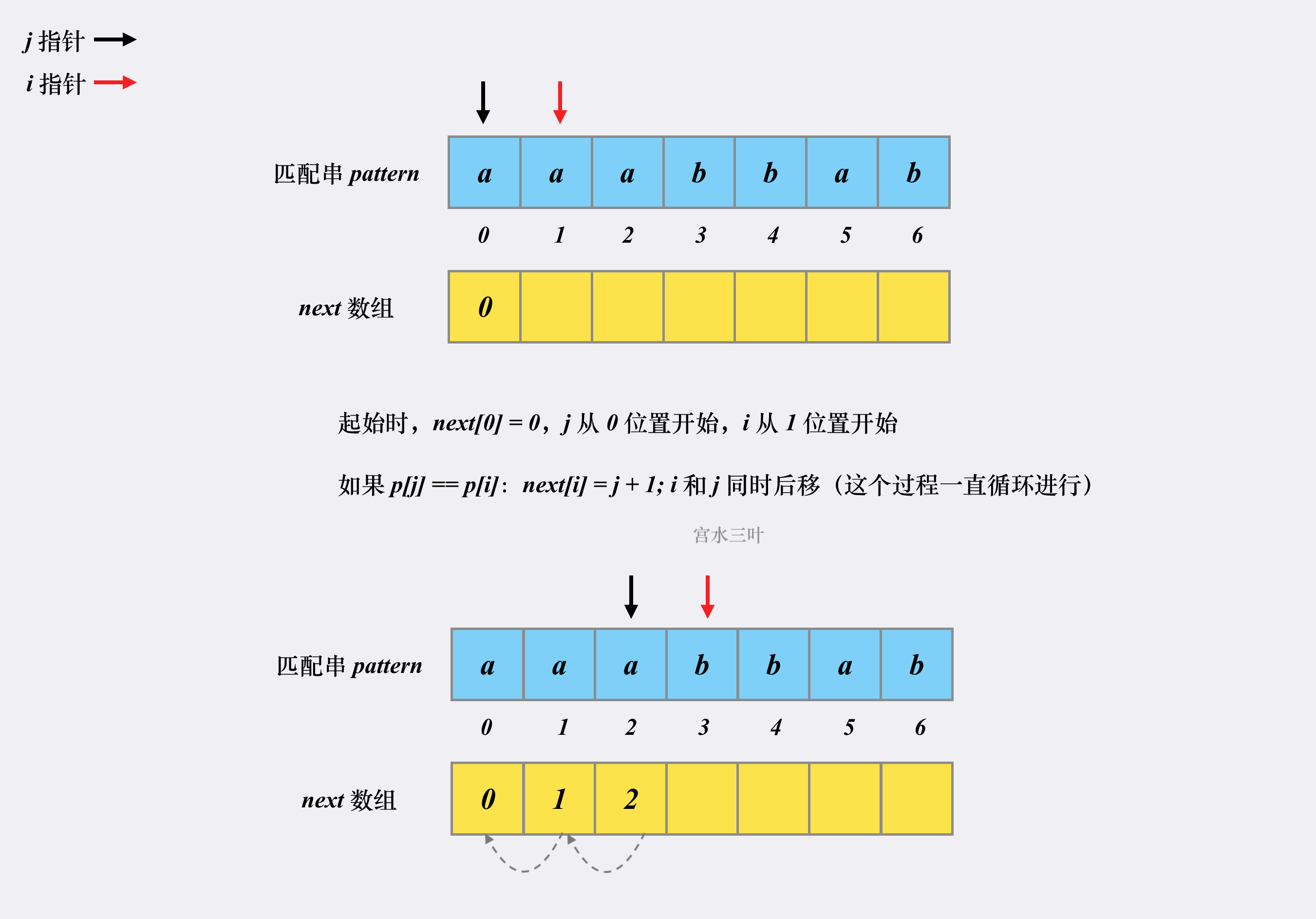
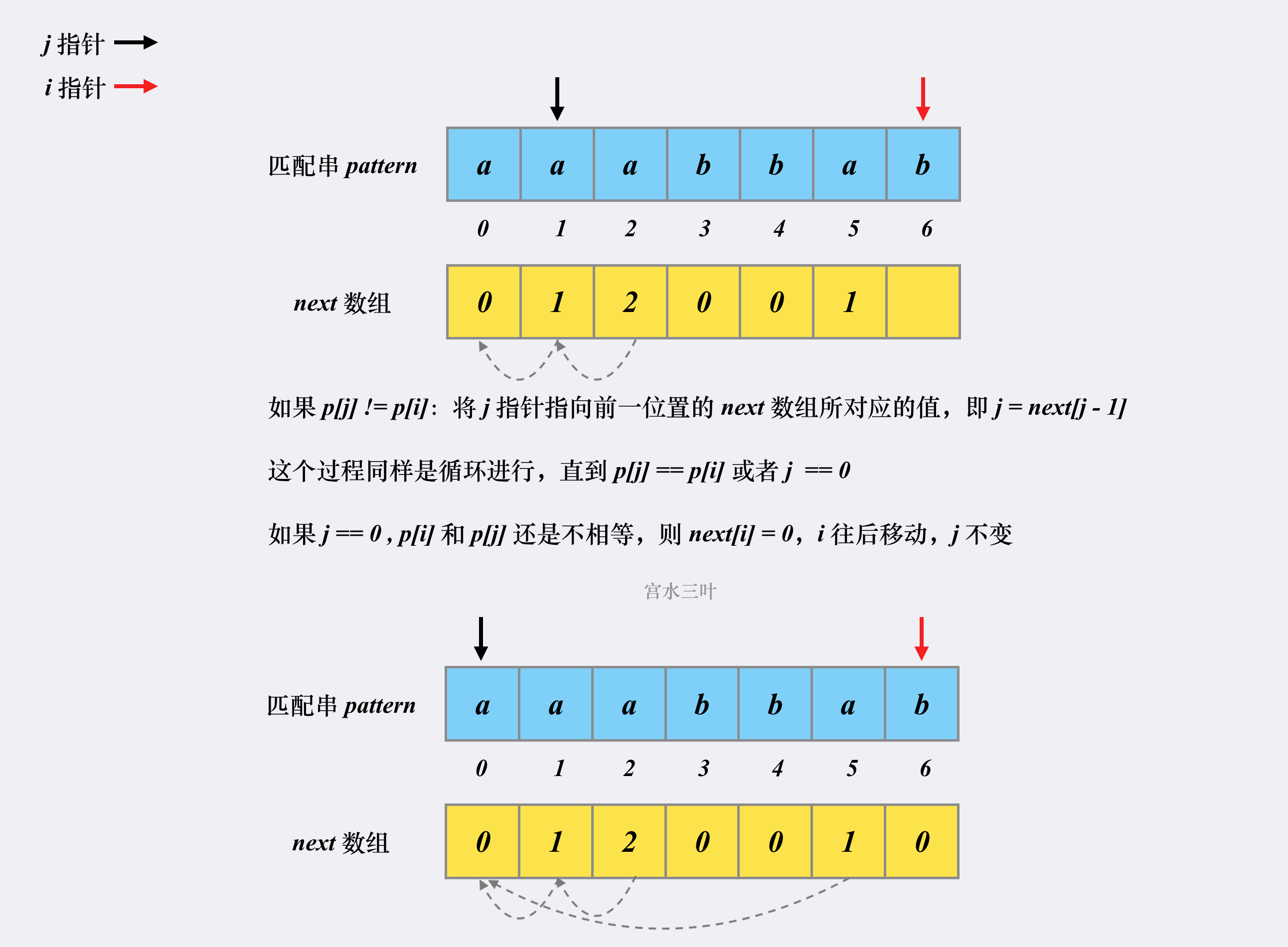
这就是整个 next 数组的构建过程，时空复杂度均为 O(m)。

至此整个 KMP 匹配过程复杂度是 O(m + n) 的。

next数组实现部分代码如下：

int n = haystack.size();
int m = needle.size();
vector<int> next(m);
next.push_back(0);
        
for (int i = 1, j = 0; i < m; i++)
{
	while (j && needle[j] != needle[i])j = next[j - 1];
	if (needle[i] == needle[j])j++;
	next[i] = j;//实现递增的效果
}

代码实现

在实际编码时，通常我会往原串和匹配串头部追加一个空格（哨兵）。

目的是让 j 下标从 0 开始，省去 j 从 -1 开始的麻烦。

class Solution {
public:
    int strStr(string s, string p) {
        int n = s.size(), m = p.size();
        if(m == 0) return 0;
        //设置哨兵
        s.insert(s.begin(),' ');
        p.insert(p.begin(),' ');
        vector<int> next(m + 1);
        //预处理next数组
        for(int i = 2, j = 0; i <= m; i++){
            while(j and p[i] != p[j + 1]) j = next[j];
            if(p[i] == p[j + 1]) j++;
            next[i] = j;
        }
        //匹配过程
        for(int i = 1, j = 0; i <= n; i++){
            while(j and s[i] != p[j + 1]) j = next[j];
            if(s[i] == p[j + 1]) j++;
            if(j == m) return i - m;
        }
        return -1;
    }
};

参考：阮一峰

图片源自水印