【算法】二维前缀和之矩形区域不超过K的最大数值和

发表于 | 分类于
字数统计: 1.1k 字 | 阅读时长 ≈ 5 分钟

问题：

给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。

题目数据保证总会存在一个数值和不超过 k 的矩形区域。

示例 1：

1
2
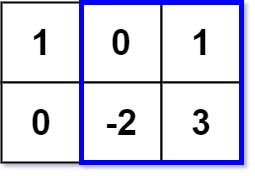
3
输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。

示例 2：

1
2
输入：matrix = [[2,2,-1]], k = 3
输出：3

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -100 <= matrix[i][j] <= 100
  • -105 <= k <= 105

前置知识：二维前缀和

二维前缀和数组中的每一个格子记录的是「以当前位置为区域的右下角（区域左上角恒定为原数组的左上角）的区域和」

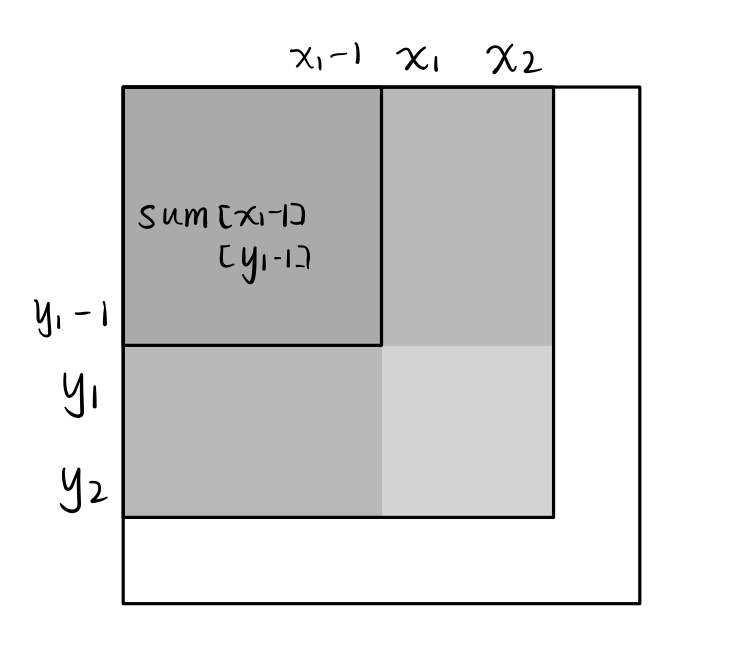
如果觉得不清晰，请将将 f[i][j] 理解成是以 (i, j) 为右下角，(0, 0) 为左上角的区域和。

因此当我们要求 (x1, y1) 作为左上角，(x2, y2) 作为右下角 的区域和的时候，可以直接利用前缀和数组快速求解：

1
sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class NumMatrix {
    int[][] sum;
    public NumMatrix(int[][] matrix) {
        int n = matrix.length, m = n == 0 ? 0 : matrix[0].length;
        // 与「一维前缀和」一样，前缀和数组下标从 1 开始，因此设定矩阵形状为 [n + 1][m + 1]（模板部分）
        sum = new int[n + 1][m + 1];
        // 预处理除前缀和数组（模板部分）
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
            }
        }
    }

    public int sumRegion(int x1, int y1, int x2, int y2) {
        // 求某一段区域和 [i, j] 的模板是 sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];（模板部分）
        // 但由于我们源数组下标从 0 开始，因此要在模板的基础上进行 + 1
        x1++; y1++; x2++; y2++;
        return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
    }
}
  • 时间复杂度：预处理前缀和数组需要对原数组进行线性扫描，复杂度为 O(n * m)，计算结果复杂度为 O(1)。整体复杂度为 O(n * m)
  • 空间复杂度：O(n * m)

解题思路：

朴素二位前缀和：

搜索所有子矩阵需要枚举「矩形左上角」和「矩形右下角」，复杂度是 O(m^2 * n^2)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
		int m=mat.size(),n=mat[0].size();
        for(int i=1;i<m;i++)
        {
			for(int j=0;j<n;j++)
            {
                sum[i][j]=sum[i-1][j]+mat[i-1][j-1]-sum[i][j-1]-sum[i-1][j-1];
            }
        }
        
        int ans=INT_MIN;
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                for(int p=i;p<=m;p++)
                {
                    for(int q=j;q<=n;q++)
                    {
                        int cur=sum[p][q]-sum[i-1][q]-sum[p][j-1]+sum[i-1][j-1];
                        if(cur<=k)
                        {
                            ans=max(ans,cur);
                        }
                    }
                }
            }
        }
        return ans;
    }
};
  • 时间复杂度：预处理前缀和数组复杂度为 O(m * n)，查找答案的复杂度为 O(m^2 * n^2)。整体复杂度为 O(m^2 * n^2)
  • 空间复杂度：O(m * n)O(m∗n)

优化：前缀+二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> sum(m + 1,vector<int>(n + 1,0));
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        int ans = INT_MIN;
        for(int top = 1; top <= m; top++){
            for(int bot = top; bot <= m; bot++){
                set<int> st;
                st.insert(0);
                for(int r = 1; r <= n; r++){
                    int right = sum[bot][r] - sum[top - 1][r];
                    auto left = st.lower_bound(right - k);
                    if(left != st.end()){
                        int cur = right - *left;
                        ans = max(ans,cur);
                    }
                    st.insert(right);
                }
            }
        }
        return ans;
    }
};
  • 时间复杂度：枚举上下边界复杂度为 O(m^2)；枚举右边界为 O(n)O(n)，使用 TreeSet（基于红黑树）存储和查找左边界复杂度为 O(log n)。整体复杂度为O(m^2∗nlogn)
  • 空间复杂度：O(m * n)

参考：AC_OIer

0%