【论文】翻译：基于顶点权重的 p-center 问题禁忌搜索

摘要

p中心问题包括从一组候选项中选择p个中心，以最大程度地减少任何客户端与其指定中心之间的最大距离。在本文中，我们将p中心问题转化为一系列覆盖子问题，并提出了一种基于顶点加权的禁忌搜索（VWTS）算法来解决这些问题。提出的VWTS算法融合了不同特征例如顶点权重技术和禁忌搜索策略，以帮助搜索跳出局部最优值。在138个最常用的基准实例上进行的计算实验表明，尽管VWTS简单易行，但与最新技术相比，它具有很高的竞争力。作为已经研究了半个多世纪的众所周知的NP难题，打破这些经典数据集的记录是一项艰巨的任务。然而，VWTS改善了54个大型实例中14个的最著名结果，并匹配了其余84个实例的最佳结果。另外，VWTS所花费的计算时间比文献中的其他算法要短得多。

1 introduction

作为Hakimi [1964]提出的经典组合优化问题，p中心问题包括从一组候选中心中选择p个中心来服务一组客户，其中每个客户由其最接近的中心之一服务。如果中心为客户服务，则存在服务弧，最长服务弧的长度为覆盖半径。这个问题的目的是使覆盖半径最小。

p中心问题在现实世界中有广泛的应用。例如，可以将城市规划中的几个重要问题表述为p中心问题，例如确定应急中心（Toregas等，1971）和消防站（Tansel等，1983）的位置。 Badri等，1998]。关于供应链管理，可以将生产工厂的位置和仓库分配建模为p中心问题[Amiri，2006]。在电信领域，p中心问题可以表述可靠的集线器网络设计问题[Tran等，2016]。

作为一个具有挑战性的NP难题[Kariv and Hakimi，1979]，在过去的几十年中，p中心问题引起了学术界的广泛关注。 p中心问题的求解方法主要可分为精确算法和元启发式算法。关于确切的算法，Minieka [1970]将p中心问题转换为一系列覆盖问题。 Daskin [2002]基于Minieka [1970]，使用拉格朗日松弛法解决了p中心问题。 Ilhan等 [2002]提出了一种算法，该算法通过优化原始问题的线性松弛来找到下界，然后通过整数规划证明一系列决策问题的不可行性来改善该下界。 Elloumi等 [2004]独立设计了与Ilhan等人类似的方法。 [2002]并获得了较好的结果。 Calik和Tansel [2013]提出了整数规划公式和基于分解的精确算法来解决p中心问题。

除了精确的方法外，还提出了各种元启发式算法来解决p中心问题。 Mladenovic等[2003]提出了禁忌搜索和变量邻域搜索。 Caruso等[2003]提出了一种混合算法，可以有效地解决一些小规模的p中心实例。 Pullan [2008]提出了一种模因算法，该算法结合了局部搜索过程和基于种群的元启发式算法。 Davidovi´c等[2011]通过蜂群优化解决了p中心问题。 Ferone等[2017]提出了一种基于GRASP的算法，Yin等人[2017]将路径重新链接与GRASP结合以解决p中心问题。

本文提出了一种基于顶点加权的禁忌搜索（VWTS）算法，该算法结合了顶点加权技术和禁忌搜索程序来解决p中心问题。与直接解决原始问题的先前元启发法不同，VWTS将p中心问题转换为一系列集合覆盖问题。具体而言，对于每个可能的覆盖半径r，它检查覆盖范围r内的任何中心是否可以服务每个客户。我们的贡献可以总结如下：

1）我们将p中心问题转换为一系列决策子问题，将每个子问题进一步转换为新的优化问题以降低复杂性。

2）通过将顶点加权技术与禁忌搜索过程相结合，并使用增量邻域评估，VWTS尽管简单易用，但在开发和探索之间达到了更好的平衡。

3）对总共138个最常用的p中心问题实例进行了测试，提出的VWTS算法提高了14个实例的最佳已知结果，并与其余实例的记录匹配。而且，我们的计算时间比文献中最先进的算法要短得多。

4）我们进行了广泛的实验，以证明我们算法关键要素的优劣，分别是顶点加权技术(VWTS)，禁忌搜索策略(tabu search strategy)和增量邻域评估(the incremental neighborhood evaluation)。

2 问题描述和转化

P-中心问题定义在无向完全图$G=(V,C,E)$上，其中$V\cup C$是顶点集，$E$是边集。每个顶点$V_i\in V$对应于$n$个要从$m$个候选中心$C$中选择出来的$p$个中心点之一服务的客户之一。对于每个连接顶点$i$和$j$的边，$d_{ij}$表示它的长度。解向量可以被定义为$(x,y,r)$，其中变量$x_j=1$当且仅当一个候选中心$j\in C$打开，变量$y_{ij}=1$当且仅当候选中心$j\in C$服务客户$i\in V$，变量$r\in R^+$是覆盖半径的上限。然后就可以将用于P-中心问题的经典混合整数编程（MIP）模型表达为以下模型（PC）。

$(PC){\quad}min{\quad}r,\tag{1}$ \[ \begin{align} s.t.&\sum_{j\in C}{x_j}\leq p,\tag{2}\\ &\sum_{j\in C}{y_{ij}}=1,\forall i\in V,\tag{3}\\ &y_{ij}≤ x_j,∀i ∈ V,∀j ∈ C,\tag{4}\\ &\sum_{j∈C}{d_{ij}y_{ij}}≤ r,∀i ∈ V,\tag{5}\\ &x_j, y_{ij}∈ \{0,1\}, r ∈ R^+,∀i ∈ V,∀j ∈ C.\tag{6} \end{align} \] 在模型$（PC）$中，目标$（1）$旨在最小化覆盖半径。约束$（2）–（5）$要求最多有p个开放的中心，每个客户必须由一个中心精确地服务，只有开放的中心可以为客户提供服务，并且覆盖范围半径不短于客户分别到达其指定的中心的任何服务弧。显然，最佳覆盖半径必须与某个边$d_{ij}$的长度相同。因此，令$Γ= \{r_1，r_2，...，r_k\}$是不同边长的有序列表，其中$r_1 <r_2 <... <r_k$，则p-center问题可被视为寻求最小边长$q$，从而使模型$(PC)$当$r≥r_q$时仍然可行，而如果添加约束$r≤r_{q-1}$则不可行。

当给出实例的最佳边缘长度实例q时，p中心问题等同于集合覆盖问题[Chvatal，1979]。具体来说，我们使用一个顶点集$V^q_j = \{i∈V |d_{ij}≤r_q\}$来表示候选中心$j∈C$可以在覆盖半径$r_q$内服务的一组客户。因此，我们可以获得一个覆盖实例$V^q = \{V^q_1，V^q_2，...，V^q_m\}$的集合。如果$V^q$中存在p个集合，它的并集包含所有的顶点，我们可以声称相应的p个中心能够为覆盖半径$r_q$内的所有客户提供服务。因此，因此，集合覆盖问题由方程定义。当给定最优边长q时，以下模型$（SC_q）$中的$（7）–（10）$等效于模型$（PC）$，其中$u_i$是二进制变量，如果客户$i$没有任何中心覆盖，则$u_i$为$1$，并且 $x_j$是模型$（PC）$中的相同决策变量。

$(SCq){\quad}min{\quad}\sum\limits_{i∈V}{ui},\tag{7}$ \[ \begin{align} s.t.&\sum_{j∈C,d_{ij}≤r_q}x_j≥ 1 − u_i,∀i ∈ V,\tag{8}\\ &\sum_{j∈C}x_j= p, \tag{9}\\ &x_j, u_i∈ \{0,1\},∀i ∈ V,∀j ∈ C.\tag{10} \end{align} \] 模型$（SC_q）$与标准集覆盖模型或Elloumi等人提出的MIP模型略有不同 [2004]。与其减少选择的集合的数量，不如通过精确地打开等式中所示的 $p$ 个中心来最小化未发现的客户的数量$（7）$。约束条件$（8）$确保每个客户在覆盖半径$r$内至少有一个中心。约束（9）限制了打开的中心数。不幸的是，我们通常缺乏关于最佳覆盖半径的先验知识，因此我们需要遍历不同的边长列表Γ来检查每个可能的半径。实际上，通过利用原始问题的边界，可以大大减少子问题的数量。

3 基于顶点加权的禁忌搜索

为了解决p-中心问题，提出的VWTS算法结合了禁忌搜索策略和顶点加权技术，解决了一系列子问题。 VWTS在有限的时间内，通过执行模型$（PC）$的求解器（如PBS算法[Pullan，2008]）获得的上限$r_{q^0}$开始，VWTS求解模型$（SC_{q^0-1}），（SC_{q^0-2}），...，（SC_1 ）$，直到在给定的时间限制内找不到模型$（SC_{q^∗ −1}）$的任何可行解。那么，$r_{q^∗}$是找到的最佳覆盖半径。因此，我们的重点将放在给定半径$r_q$的模型$（SC_q）$的求解方法上。提议的VWTS算法的主要框架在算法1中提出。它通过贪婪算法（第1行）生成初始解X，并通过禁忌搜索程序（第4-14行）迭代地改善现有解决方案。在VWTS算法的每次迭代中，它首先评估当前解决方案的邻域并记录最佳邻域移动，同时注意其禁忌状态（第5行）。然后，它会采取最佳移动，并用得到的相邻解决方案替换当前解决方案（第6行）。如果当前解决方案$X$改善了迄今为止找到的最佳解决方案，则$X^*$将更新为$X$（第7-8行）。否则，我们需要检查当前解决方案是否处于局部最优，也就是说，函数FindPair()返回的最佳移动不能减少未发现的客户的数量（第9行）。如果出现停滞，则将调整每个未覆盖客户的权重（第10行）。最后，当满足指定的终止条件时，算法终止并返回最佳解$X^*$。

Algorithm 1 VWTS算法的主要框架 Input: 图$G$，中心数$p$，覆盖半径$r_q$ Output: 目前找到的最佳解决方案$X^*$

1: A set of p centers X ← Init(G, p, rq) /* (Section 3.1) */
2: X∗← X, X0← X, tabu list T L ← ∅, iter ← 1
3: V ertex weights wi← 1,∀i ∈ V /* (Section 3.2) */
4: while termination condition is not met do
5: 		(i, j) ← FindPair(X’, T L, iter) /* (Algorithm 2) */
6: 		MakeMove(i, j) /* (Algorithm 4) */
7: 		if |U(X)| < |U(X∗)| then /* U(X) is the set of */
8: 			X∗← X /* clients uncovered by X */
9: 		else if |U(X)| ≥ |U(X0)| then
10: 		wv← wv+ 1,∀v ∈ U(X) /* (Section 3.2) */
11: 	end if /* more uncovered clients than last solution */
12: 	T L ← {i, j} /* update tabu list (Section 3.4) */
13: 	X‘← X, iter ← iter + 1
14: end while

3.1 初始化

VWTS算法采用构造启发式生成一组中心$X$作为初始解。让$V_j$表示候选中心$j$在当前覆盖半径内可以服务的客户集合。给出能够为客户$i$服务的候选中心集合，即$C_i= \{j∈C|i∈V_j\}$。$U(X) = V \setminus \bigcup_{ j∈x} V_j$表示解决方案$X$中未服务的客户的集合。在最大覆盖原则下，建设性启发式逐个开放中心。即迭代选择覆盖大部分未发现客户端的候选中心$j = arg{\quad}max_{j∈C\setminus X}|V_j∩U(X)|$，并插入当前解决方案$X$中。如果有多个候选中心覆盖相同数量未发现客户端，则关系会随机断开。该结构的时间复杂度为$O(np)$。

3.2顶点加权技术

顶点加权技术通过改变目标函数来帮助搜索脱离局部最优。它可以看作是引导局部搜索的一种变化[Voudouris和Tsang, 2003]，并已成功应用于许多问题，如单点集覆盖问题[Gao等人，2015]，最小顶点覆盖问题[Cai等人，2011]和可满足性问题[Luo等人，2012]。在p-中心问题中，我们根据Eq.(11)调整目标(7)。 \[ \begin{align} (SC^w_q) {\quad} &min f(X) =\sum_{∀i∈V}w_iu_i, \tag{11}\\ &s.t. (8)–(10). \end{align} \] 因此，VWTS算法实际上是在模型$(SC^w_q)$上工作的。注意，它是一个动态模型，随着搜索的进行$w_i$会发生变化。如果VWTS算法一直没有覆盖到某个客户，这意味着这个顶点很难覆盖，我们应该以更高的优先级来处理它。具体来说，当禁忌搜索陷入局部最优解$X$时，VWTS算法将每个未被发现的客户$i∈U(X)$的权重$w_i$增加一个单位(算法1，第9-11行)。然而，无论权重的配置如何，最优解的目标值总是零。这个过程改变了解决方案空间的格局，使$X$不再是局部最优，使这个搜索过程将能够继续探索其他搜索领域。遇到停滞时，客户端在$U(X)$中出现的频率越高，其权重越大。一方面，顶点加权技术能够防止顶点被重复发现，以一种自适应的方式使搜索多样化;另一方面，对解空间进行平滑修改，将搜索引导到有希望的搜索区域。

3.3邻域结构与评价

为了改进模型$(SC^w_q)$下的初始解，VWTS采用了一种基于交换的邻域结构，该结构受大多数基于本地搜索的元启发式方法启发而解决了p-center问题[Pullan，2008]，而邻域评估由于在第2节和以下加速策略中提出了重新制定的方法。用$Swap(i，j)$表示，通过打开候选$i∈C \setminus X$并关闭打开的中心$ j∈X$，一次交换移动可产生相邻解$X⊕Swap（i，j）= X∪{i} {j}$

在基于轨迹的元启发式算法中，邻域评估是最耗时的过程。对于采用最佳改进策略的典型禁忌搜索算法，它会在每次迭代时评估所有可行的移动，并执行最佳邻域移动之一，从而尽可能提高目标值。由于存在$O（p（n-p））$交换移动，因此在某些大型实例上，邻域的大小可能会很大。因此，我们使用邻域采样策略和增量评估技术来加速评估。

一方面，只能通过覆盖一些未覆盖的客户端来提高目标值，因此，如果$i$覆盖了$U（X）$中的一些未覆盖顶点，则VWTS算法将仅评估交换移动$Swap（i，j）$。由于必须最终覆盖每个客户，因此VWTS算法随机选择一个顶点$k∈U（X）$，仅评估邻点移动$Swap（i，j）$，其中$i∈C_k$ 且 $j∈X$。评估中，搜索的多样化作为一个副作用得到了改善，在集约化和多样化之间达到了更好的平衡。

另一方面，我们尝试通过重用一些中间结果计算目标值来加速邻域评估。 VWTS并非根据目标（11）对被覆盖客户的权重求和，而是通过存储和维护$δ_j$来增量评估所有邻域移动，而通过关闭（打开）中心$j$来增加（减少）目标值。对于每个中心$j∈X$，$δ_j= \sum_{i∈(V_j∩U(X \setminus \{j\}))}w_i$是只能由中心$j$服务的顶点权重之和。对于每个候选中心$j \notin X$，$δ_j= \sum_{i∈（V_j∩U（X））}w_i$是$V_j$中所有未发现客户的权重之和。然后，可以以$O（1）$时间复杂度来实现对每个邻域移动的评估，但代价是每次打开或关闭中心后都会更新受影响的$δ$值。具体地，通过$f（X∪\{i\}）＝ f（X）-δ_i$来计算开放中心$i$的目标值。

然后，我们需要更新受打开中心$i$影响的$δ$值，这消除了由于覆盖范围重叠而关闭某些中心的惩罚。之后，我们可以通过$f（X⊕Swap（i，j））= f（X∪\{i\}）+δ_j$来评估相邻解。由于禁忌搜索过程评估计算步数很多，但每次迭代仅执行一次移动，因此值得维护和查询缓存，而不是为每个交换移动从头计算目标函数。

算法2描述了邻域评估过程。它随机选择一个客户$k∈U（X）$（第4行），并尝试打开每个覆盖顶点$k$的候选中心（第6-7行）。子例程$TryToOpenCenter（i）$保留每个最新的$δ_j$，以加快目标函数$f（X⊕Swap（i，j））$的计算。对于每个非禁忌邻域解决方案，如果其目标值小于$obj$，则将相应的邻域移动保存为最佳移动（第9-16行）。当评估了关于开设候选中心$i$的所有试验动作时，我们需要恢复$δ$值（第18行）。

Algorithm 2 找到最佳交换对

1: function FINDPAIR(X, T L, iter)
2: 		The set of best swap moves M ← ∅
3: 		The best objective value obj ← +∞
4: 		v ← a randomly picked uncovered vertex in U(X)
5: 		δ’j← δj,∀j ∈ C /* backup before trial moves */
6: 		for all i ∈ Cv do /* Cv: candidates covering v */
7: 			TryToOpenCenter(i)  /* (Algorithm 3) */
8: 			for all j ∈ X do /* evaluate closing center j */
9: 				if {i, j} ∩ T L = ∅ then /* not tabu move */
10: 				if f(X ⊕ Swap(i, j)) < obj then
11: 					obj ← f(X ⊕ Swap(i, j))
12: 					M ← {Swap(i, j)}
13: 				else if f(X ⊕ Swap(i, j)) = obj then
14: 					M ← M ∪ {Swap(i, j)}
15: 				end if
16: 			end if
17: 		end for
18: 		δj← δ’j,∀j ∈ C /* restore after trial moves */
19: 	end for /* v ∈ U(X) ⇔ Cv∩ X = ∅ */
20: 	return a randomly picked move in M
21: end function

显然，覆盖已经覆盖的客户$v（| X∩C_v |≥1）$不会提高目标值，并且如果有多个中心可以覆盖顶点$v（| X∩C_v |≥2）$，关闭为客户$v$服务的中心也不会恶化目标值。因此，如算法3所示，如果在打开中心$i$之前恰好有一个中心$l$覆盖了客户端$v（| X∩C_v | = 1）$，那么用于关闭客户端$v$的关闭中心$l$的$δ$值将通过$w_v$减小（第4-7行），因为一旦中心$i$打开，关闭的中心$l$不会使客户$v$被发现。我们只对$δ_j（∀j∈X）$关闭一个中心感兴趣，因为算法2中的第8-17行仅涉及闭合另一个中心。因此，算法2和算法3的最坏情况时间复杂度分别为$O（n2）$和$O（n）$。

Algorithm 3 模拟打开一个中心

1: function TRYTOOPENCENTER(i)
2: 		for all v ∈ Vi do /* |X ∩ Cv|: number of centers */
3: 			if |X ∩ Cv| = 1 then /* covering v in X */
4: 				/* cancel penalty for making v uncovered */
5: 				δl← δl− wv,for l ∈ X ∩ Cv  /* O(1) */
6: 			end if /* l was the only center covering v but */
7: 		end for /* it will not be the only one if i opens so */
8: end function /* closing l does not make v uncovered */

当执行最佳交换移动时（算法1，第6行），我们需要调用算法4来更新受影响的数据结构。除了将$δ$值更新为算法3(第3 - 4行)，如果在打开中心$i$之前没有中心覆盖客户端$v(|X∩C_v| = 0)$，那么打开每个候选中心$l$覆盖客户端$v$的$δ$值减少$w_v$(第5-7行)，因为打开的中心$l$已经覆盖了已覆盖的客户$v$ ,未来$l$将不再通过$w_v$提高目标价值。然后，更新开放中心的集合(第9行)。闭合中心$j$对$δ$值的影响以类似的方式考虑(第10-16行)。

Algorithm 4 互换移动

1: function MAKEMOVE(i, j)
2: 		for all v ∈ Vi do /* consequences of opening i */
3: 			if |X ∩ Cv| = 1 then /* (Algorithm 3) */
4: 				δl← δl− wv,for l ∈ X ∩ Cv
5: 			else if |X ∩ Cv| = 0 then
6: 				δl← δl− wv,∀l ∈ Cv\ {i}
7: 			end if /* cancel reward for covering v */
8: 		end for
9: 		X ← X ∪ {i} \ {j}
10: 	for all v ∈ Vj do /* consequences of closing j */
11: 		if |X ∩ Cv| = 0 then /* add reward for */
12:				 δl← δl+ wv,∀l ∈ Cv\ {j} /* covering v */
13: 		else if |X ∩ Cv| = 1 then
14: 			δl← δl+ wv,for l ∈ X ∩ Cv
15: 		end if /* add penalty for uncovering v */
16: 	end for
17: end function

3.4 Tabu Search

禁忌搜索通常包含一个基于新近度的禁忌列表（recency-based tabu list），以禁止重新访问最近访问过的解决方案。禁忌策略防止立即关闭新开设的中心或重新开放新关闭的中心。我们将禁忌策略中的禁忌保留区参数固定为一次迭代，因此所提出的算法保持简单且无参数。具体来说，如果我们在当前迭代迭代中打开（关闭）一个中心，则禁止在下一次迭代中再次关闭（打开）它。因此，迭代 $iter$ 时的 $Swap(i, j)$ 在禁忌列表 $TL$（算法 1，第 12 行）中引入了两个顶点 $\{i, j\}$，并且在迭代 $iter + 1$（算法 2，第 9 行）时不能涉及 $i$ 和 $j$ .

4 实验结果与比较

为了评估所提出的 VWTS 算法的有效性，我们在众所周知的数据集上进行了大量实验，并将 VWTS 与 T goy-第九届国际人工智能联合会议 (IJCAI-20) 艺术算法的最新进展进行了比较包括两种精确算法（ELP [Elloumi et al., 2004] 和 DBR2 [Calik and Tansel, 2013]）和三种元启发式算法（PBS [Pullan, 2008]、GRASP+PS [Ferone et al., 2017] 和 GRASP /PR [Yin et al., 2017])。

4.1 实验协议

我们提出的 VWTS 算法是用 C++ 编程并用 Visual Studio 2017 编译的。所有实验都在 Windows Server 2012 x64 上进行，使用 Intel Xeon E52609v2 2.50 GHz CPU。我们在 5 毫秒的时间限制下运行重新实现的 PBS 算法 [Pullan，2008]，以获得每个实例的覆盖半径 $r_{q^0}$ 的良好初始上限。我们对每个实例进行了 20 次独立运行，每个覆盖半径引起的每个子问题的截止时间为 6 分钟。由于参考算法的程序不可用，我们在相应的论文中报告了它们的计算时间，并根据 CPU 频率对运行时间进行了标准化，以进行公平比较。 ELP 的运行时间除以 6.25，因为它在 400 MHz Pentium II CPU 上运行。其余算法在更快（PBS、GRASP+PS、GRASP/PR）或未知 (DBR2) CPU 上进行测试，因此我们按原样报告它们的计算时间。

p中心问题主要有两组基准实例。第一组由来自 OR-Library [Beasley, 1990] 的 40 个小实例 (pmed) 组成。第二组包含来自 TSPLIB 的 98 个实例，这些实例基于平面图并从现实世界的应用程序[Reinelt, 1991] 派生而来。 TSPLIB 数据集可以进一步分为 44 个小于 1000 个顶点的小实例（sTSP）和 54 个大实例（u1060、rl1323、u1817、pcb3038）。在这些情况下，客户也是候选中心$（V = C）$。我们通过 Floyd 算法 [Floyd, 1962] 为 pmed 实例计算所有对最短路径，并将 TSPLIB 实例的欧几里德距离四舍五入到最接近的百分之一，就像 Pullan [2008] 所做的那样。请注意，算法 ELP 和 DBR2 采用整数距离，这太粗糙而无法找出最佳 $q^*$。

4.2 计算结果

在本节中，我们对VWTS算法的性能进行了全面的研究，并在表1和表2中报告了详细的结果。它们遵循下面描述的相同惯例。列“数据集”和“实例”分别给出数据集和实例的名称。列$n$和列$p$分别表示顶点和中心的数量。列"计数"表示数据集中的实例数。列CPU给出标准化的平均CPU时间(以秒为单位)。对于VWTS，它包括计算$r_{q^0}$和依次解决从$(SC_{q^0})$到$(SC_{q^∗})$的所有子问题的总时间。列$CPU-q^∗$报告VWTS的运行时间(以秒为单位)，以解决由最知名的覆盖半径$r_{q^∗}$引起的子问题，这显示了并行计算可用时VWTS的极限。$f_{best}$列表示通过相应算法得到的最佳客观值。第#best列显示了对应算法匹配最佳已知结果的实例数。#better、#equal和#worse分别表示VWTS与相应算法相比获得更好、相等和更差结果的实例数。

表1比较了ELP、DBR2、PBS、GRASP/PR和我们的VWTS获得的每个数据集的总体结果。我们可以看到，VWTS在所有实例中获得的已知结果都是最好的，而没有任何参考算法能够获得这样的总体结果。此外，VWTS在每个数据集上的平均计算时间比文献中最佳算法缩短了4倍以上。如果并行计算可用，性能增益可以超过30倍。时差是如此之大，以致于比较不受归一化的影响。此外，VWTS非常稳定，因为它总是在所有20次独立运行中获得报告的结果。

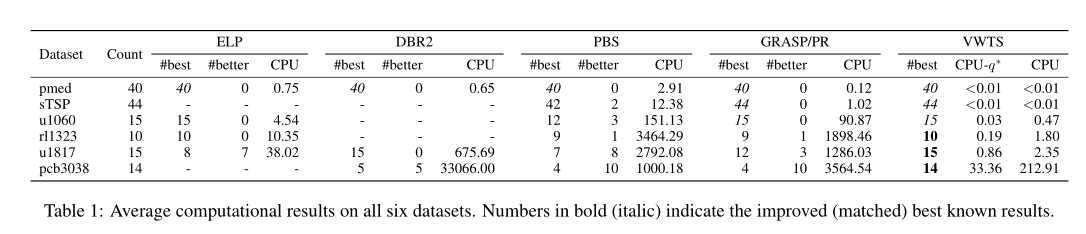
表2比较了ELP、DBR2、PBS、GRASP+PS、GRASP/PR和我们的VWTS在30个最大、最具挑战性的实例上的实验结果。请注意，数据集pcb3038的真正上界已经几十年没有更新过了(尽管DBR2改进了一些整数边界)。从表2可以看出，本文提出的VWTS算法改进了先前GRASP/PR和PBS对rl1323、u1817和pcb3038的最佳已知结果(p = 100、p = 80,130,150)。除了改进的解决方案质量，VWTS在计算时间方面优于u1817和pcb3038数据集上的所有参考算法。对于最优或最知名覆盖半径对应的子问题的运行时间，VWTS能够在3秒内对30个实例中的23个获得新的最知名结果。此外，如果VWTS停止在之前的最佳覆盖半径，它只需要3秒28个实例。总之，这些统计数据表明，我们的VWTS对于解决p-center问题是高效、健壮、并发友好的。

4.3 VWTS成分的重要性

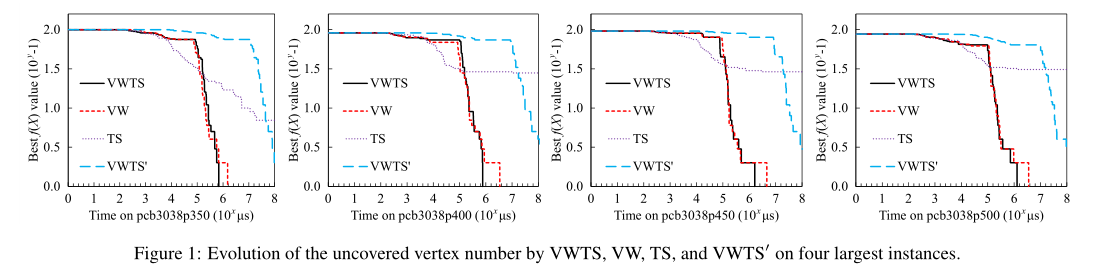
为了评价顶点加权技术、禁忌搜索策略和增量邻域评估的优点，我们在四个最大的实例(pcb3038, p = 350,400,450,500)上进行了实验，比较了禁用禁忌策略(VW)得到的VWTS的简化版本。取消顶点加权技术(TS)和使用朴素邻域评估代替增量评估(VWTS0)。

图1描述了VWTS、VW、TS和VWTS0搜索过程中未被发现的顶点数的演变。每个点(x, y)意味着有10y−1个客户端在10x微秒内没有被任何中心提供服务。我们可以看到，虽然TS在开始的毫秒内可以得到比VWTS更好的解决方案，但是VWTS和VW在0.1秒后就超越了。这一现象的原因可能是，禁忌搜索过于注重禁止候选人中心成为中心，而不是直接防止客户被发现。在极端情况下，一些难以服务的顶点将永远没有机会得到服务。而禁忌策略加速了VWTS的收敛。由图1可知，VWTS在寻找可行覆盖时比VW快了100.2= 1.5倍。此外，当禁用增量计算时，vwts0比完整算法慢100倍。这些观察结果证实了顶点加权技术、禁忌策略和增量评估在VWTS的有效性和效率方面都是必不可少的。

5 结论

本文提出了一种基于顶点加权的禁忌搜索算法来解决p中心问题。我们将 p-center 问题分解为一系列覆盖子问题的集合，并通过结合顶点加权技术和禁忌搜索策略来解决它们。 VWTS 在 138 个广泛使用的数据集上进行了测试，在 14 个实例上改进了最佳已知结果，并在更短的运行时间内匹配了所有剩余数据的文献记录。因此，将来研究用于解决其他优化问题的建议策略的组合将是有吸引力的。