本文提出了一种基于改进规则和强化学习的混合启发式算法来解决二维矩形Packing问题(2DSPP)。首先,改进了基于skyline算法的评分规则,考虑了具有一组宽度松弛因子的“两步”连续项。改进后的评分规则可以有效地减少空间浪费。其次,作为一种强化学习方法,建立了深度q网络(DQN),得到初始矩形项序列,同时作为放置规则的基本补充。它可以提高空间利用率,防止算法陷入局部最优状态。结合新的”两步”放置规则和DQN,提出了基于简单随机算法(SRA)的启发式算法,称为基于强化学习的简单随机算法(RSRA)。
模型
改进的评分规则:
\(A.w\)表示放置一个矩形块后剩余空间的宽度。\(r_{min}.w\)是剩余未放置矩形块中最小的矩形块的宽度。\(r_{min}.w ≤ A.w\)表示\(r_{min}\)可以放在这里,进一步减少空间浪费。如图 2(a)-(b) 所示,放置 \(r_1\)或\(r_2\)将得到相同的分数。图 2(c)-(d) 表明当\(r_{min}.w > A.w\)时,不可避免地会导致宽度浪费。在这种情况下,宽度较大的项目\(r_4\)将优先于\(r_3\)放置,以减少宽度浪费。
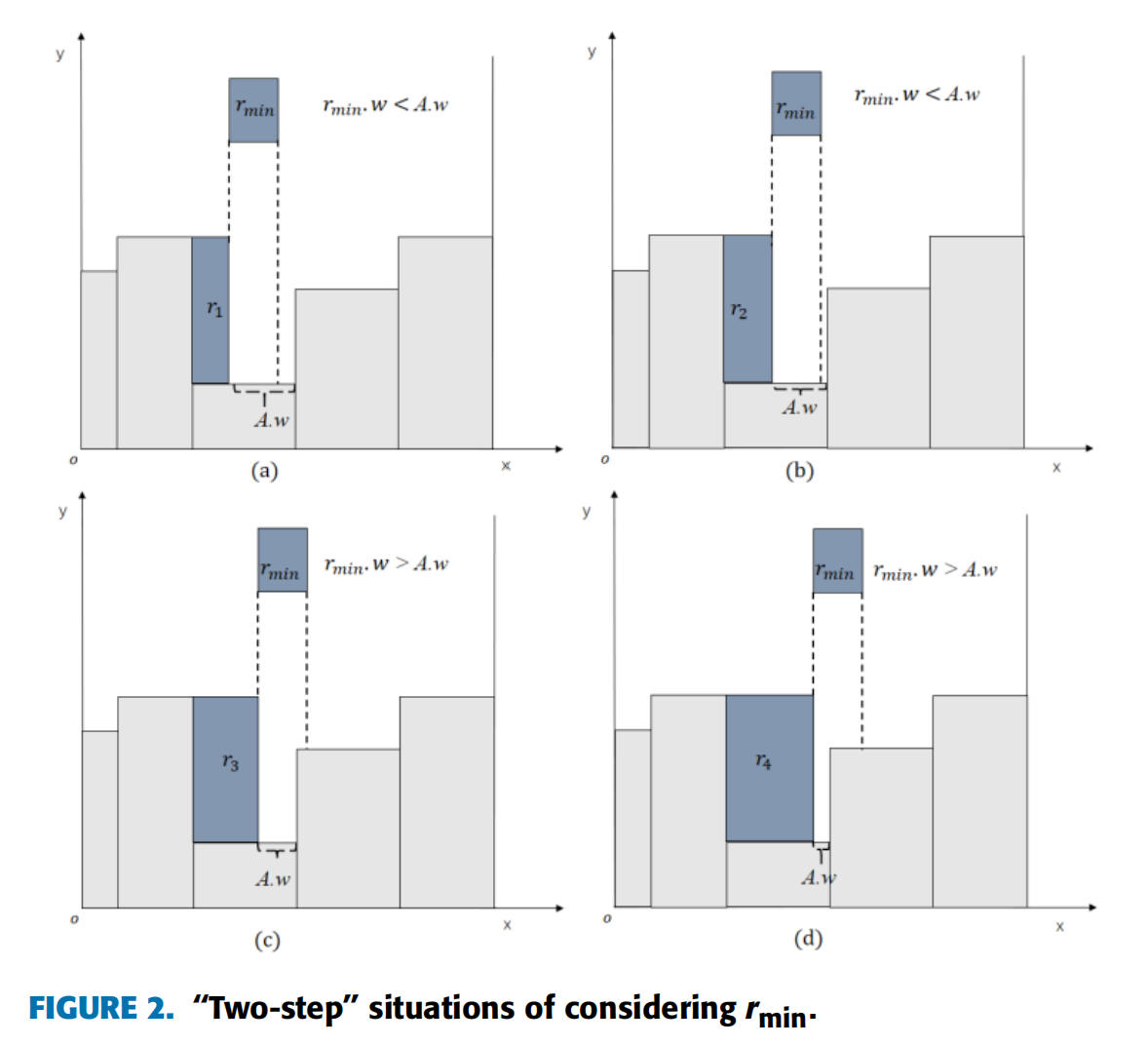
由于空间浪费在某种程度上是不可避免的,所以放置的物品越宽,适应度值应该越高。为了最大限度地减少浪费,设计了一组松弛因子\((α,β,0<α<1,0<β<1)\)在多个宽度区间内给出不同的适应度值。通过大量实验得到了最优值 \(α = 0.2\)和\(β = 0.5\)。
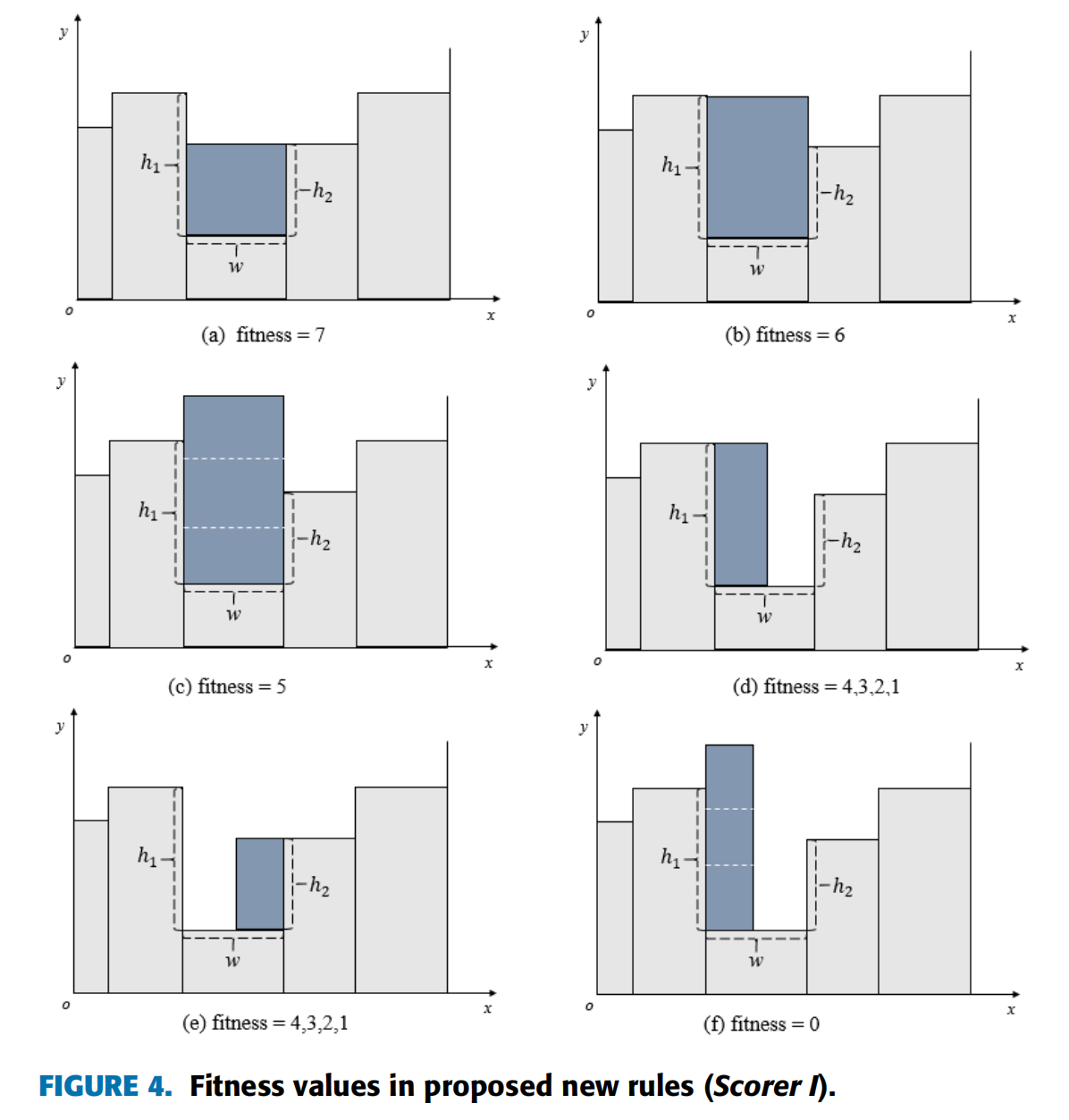
为了避免组合放置后高度值过高,我们放弃使用高度松弛因子(图3)。考虑\(r.w=s_{lowy}.w\)的两种情况如图4(a)-(b)\((r.h=h_1vs.r.h=h_2)\),将前者的适应度值设置得更高,这样可以使空间更平坦,更有利于放置下一个矩形块。
剩余规则如表1。

强化学习方法:
强化学习是基于环境反馈机制的。通过与环境的不断互动,尝试和错误,强化学习实现了整体行动的利益最大化。
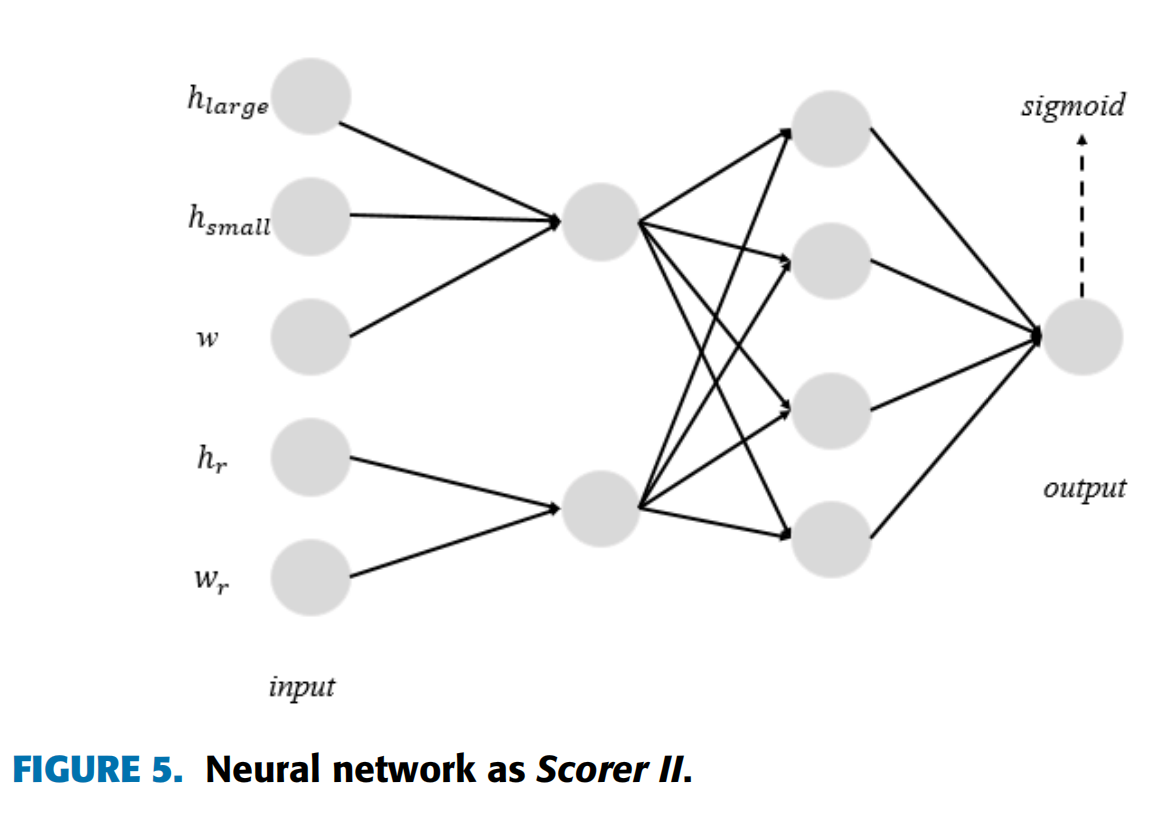
Q-learning算法是强化学习中基于value的算法之一。Q(s, a)是表示在状态s的情况下执行动作a的奖励值。Q函数在状态为s的情况下会选择最大动作执行的值。作为Q-learning算法中的表函数,Q-table不适用于2DSPP。 所以使用DQN代替Q-table进行 Q-learning。DQN的原理是使用人工神经网络来代替动作值函数。神经网络比人工特征搜索要强大得多,因为它具有很强的表达能力,可以自动提取特征。本文使用的网络结构如图5所示。
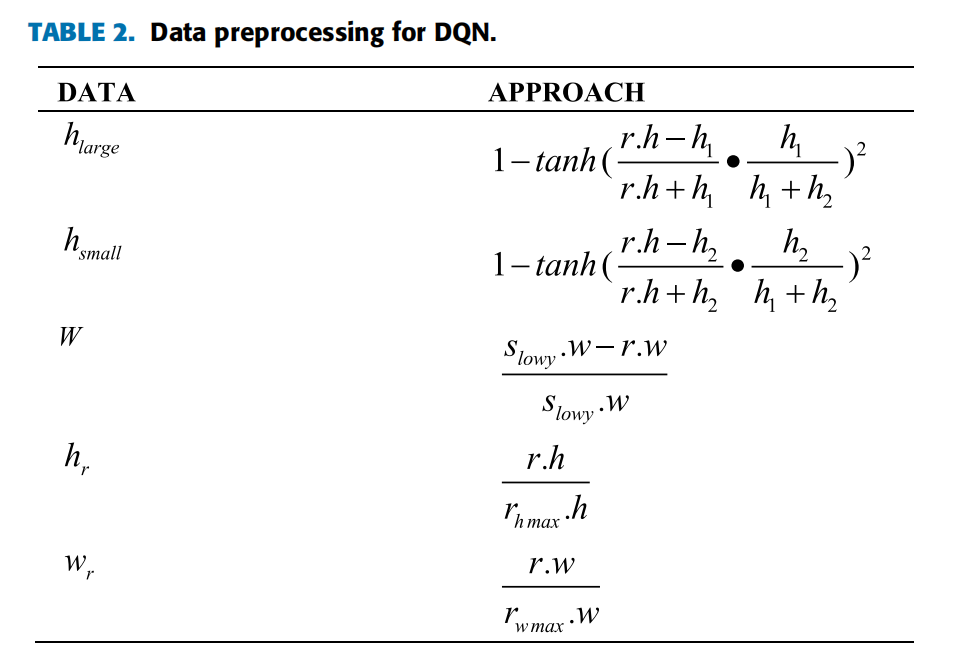
数据预处理方法如表2所示。对于输入数据,\(h_{large}\)是根据\(r.h\)和\(h_1\)之间的高度差计算的。\(h_{small}\)由 \(r.h\)和\(h_2\)之间的高度差计算得出。\(W\)是根据\(r.w\)的宽度和要放置的空间的宽度的差值来计算的。\(h_r\)是\(r.h\)与\(r_{h_{max}}.h\)的比率,\(r_{h_{max}}.h\)是剩余矩形块的最大高度。\(w_r\)是 \(r.w\)与 \(r_{w_{max}}\)的比率,\(r_{w_{max}}\)是剩余矩形块的最大宽度。
网络的输出值是矩形\(r\)与空间\(s\)的匹配度。\(h_{marge}\)、\(h_{small}\)和\(w\)三个属性通过线性变换和激活函数得到一个中间值。类似地,其他两个属性\(h_r\)和\(w_r\)也可以通过相同的操作具有相应的中间值。然后,这两个中间值首先进行2×4和激活函数tanh的线性变换,然后进行4×1和激活函数sigmoid的线性变换得到最终结果。sigmoid的值范围为\((0,1)\)。
基于DQN的启发式算法(RSRA)
DQN被用于构造评估函数。
line 1: skyline算法将在从五个index生成初始序列后分别按照:周长、面积、宽度、长度(来自 Scorer I)和 Scorer II来排序。 五个序列中最小高度的解将被保存到下一阶段。
line2: 局部搜索算法LS()将按照给定的顺序依次交换两个矩形块,并实现skyline算法,以获得一个局部最优的解决方案。
line3-19: SRA最终将用于改进解。

实验
training过程:
训练开始时,从TrainSet中随机选择n组数据,得到TrainSet*作为本次循环使用的数据集,然后将TrainSet*中的每组数据依次放置,形成一个由矩形块组成的序列R。
从\((0, num)\)中随机选择一个数m,其中num是R中的矩形块个数。使用Scorer II作为评分规则的skyline算法从R中选出m个矩形块放置。这里将最低的水平线标记为\(s_{lowy}\)。设 \(k =num - m\)。非常小的 k 值会导致 DQN 的可信度低。为 k设置阈值 t,如果\(k<t\)将跳到下一个循环。否则按照表2的数据预处理方法对此时的k项进行处理,记为\(x_j\)。
尝试将每个 $x_j (j = 1 . . . k) \(放置在\)s_{lowy}\(的位置执行skyline算法,得到最终的高度\)h_j\(。记录最大高度\)h_{max}\(和最小高度\)h_{min}$。
使用方程\(y_j=\frac{h_{max}−h_j} {h_{max}−h_{min}}\)从每个\(x_j\)计算\(y_j\)。保存所有\(x_j\)和\(y_j\)。
最后,使用保存的\(x_j\)作为输入,\(y_j\)作为目标值来训练 Scorer II。当达到设定的时间或达到最佳效果时training结束。详见算法2。
