摘要
本文研究了二维矩形包装面积最小化问题(RPAMP),其目标是将一组矩形放置到一个具有可变尺寸的容器中,并最小化容器的面积。将RPAMP转化为一系列二维条带包装问题(2DSPs)。提出了一种新的自适应选择方法,在每次迭代中选择一个候选宽度,而不是在最开始就选择最有希望的宽度集。引入了一种迭代重复搜索策略,以避免在相同的宽度上花费太多的精力。采用基于skyline的最佳拟合启发式方法解决2DSP。与以往的方法相比,所提出的方法要简单得多,因为它不需要任何控制参数。
介绍
在本文中,我们提出了一种自适应选择方法(ASA)。ASA通过固定容器的宽度,将RPAMP转换为一系列的2DSPs。ASA不是首先固定有希望的宽度集,而是在每次迭代中随机选择一个可能的宽度。每个宽度被选择的概率被自适应地更新,以确保宽度可能导致一个更好的RPAMP解被给予一个更高的概率。一种基于skyline的启发式方法适用于求解2DSP。
本文主要有三个贡献:① 我们提出了一种没有任何控制参数的自适应选择方法来解决RPAMP问题。与以前的策略相比,我们的方法更简单,更易于实现。② 我们采用了一种基于skyline的启发式方法来解决2DSP,并采用迭代加倍策略来提高效率。③ 在基准测试集上的结果表明,我们的方法优于所有现有的方法,并为大多数实例找到了新的最佳解决方案。
方法
自适应的选择宽度的方法
比起在最开始选择最有希望的候选宽度,我们不是在开始的时候过滤宽度。我们选择将所有可能的宽度添加到候选宽度集中,并在每次迭代时从这个宽度集中随机选择一个宽度。由于选择宽度可能会产生高质量的RPAMP解决方案,我们给每个宽度一个分数来衡量这个宽度可以被选择的概率。这个分数是基于通过在这个宽度上调用RandomLS所得到的最优解的填充率,并且会自适应地更新。每个宽度的初始分数被设置为通过调用RandomLS算法得到的解的填充率。在每次迭代中,根据分数随机选择一个宽度(分数越高,给出的概率越大),对所选择的宽度调用2DSP的随机局部搜索算法求解,并相应地更新该宽度的分数。为了避免在相同的宽度上花费太多的精力,我们将iter初始设置为1,并在每次迭代后iter增加一倍,迭代相同宽度的工作量将加倍。
自适应选择方法详见算法1,RandomLS过程是2DSP的一种随机局部搜索方法。我们首先计算候选宽度集W(只考虑给定范围内的宽度[Wmin,Wmax])。此外,我们还舍弃了不能表示输入矩形尺寸组合的宽度。因此,W只包含作为输入矩形的维度组合的宽度。

对于每个\(W_i\),使用一个变量\(H_i\)来记录在这个宽度上找到的最小高度,而\(fr_i\)是相应的填充比。此外,使用变量\(iter_i\)记录\(W_i\)上RandomLS最后一次调用中使用的值,初始\(iter_i\)设置为1。我们首先调用\(W\)中每个宽度上\(iter\)设置为1的RandomLS,然后,\(W\)中的宽度通过填充率增序进行排序。在每次迭代中,从\(W\)中随机选择一个宽度,选择第\(k\)个宽度的概率由\(\frac{2k}{|W|×(|W|+1)}\)计算,W中序号越大的宽度概率越高。\(W\)按填充率的增加排序,说明填充率越高的宽度概率越高。假设所选宽度为\(W_k\),它首先加倍\(iter_k\),然后在\(W_k\)上调用RandomLS,\(iter\)设置为\(iter_k\)。在RandomLS返回值后,必要时\(H_k\)、\(fr_k\)和\(W\)将被更新。最大的\(iter_k\)的值被限制为\(n\),以避免在RandomLS的一次调用中进行过多的迭代。
在每次调用宽度\(W_k\)之前,变量\(iter_k\)将加倍,以确保在相同的宽度上花费更多的精力。原因是随着过程的进行,解决方案很难得到改进,因此需要更多的迭代才能找到更好的解决方案。但是,为了避免在相同的宽度上花费太多的精力,\(iter_k\)的最大值被限制在矩形的数量\(n\)的范围内。
2DSP上的随机局部搜索算法RandomLS
算法2给出的随机局部搜索RandomLS算法被用来解决2DSP。RandomLS是一个基于序列的随机局部搜索程序,它使用一个最适应HeuristicPacking算法来构建一个放置方案。更确切地说,给定一个矩形块序列\(R\),容器的宽度\(W_k\)和控制参数\(iter\),RandomLS调用HeuristicPacking \(iter\)次,最后发现的最小高度被返回。
对于每个\(W_k\),RandomLS维护一个包含排序规则集的全局集\(sr_k\)。如果这是第一次在宽度\(W_k\)上调用RandomLS,RandomLS将首先初始化集合\(sr_k\)如下:
1.按面积降序排列;
2.按高度降序排列;
3.按宽度降序排列;
4.随机排序。(生成随机序列使搜索空间多样化)
它使用四个排序规则生成四个初始序列,并调用在每个序列上的HeuristicPacking,然后将每个排序规则添加到\(sr_k\)中。然后,\(sr_k\)按HeuristicPacking返回的高度递减顺序排序。否则,它将从\(sr_k\)中随机选择一个排序规则。以概率为\(\frac{2i}{|sr_k|×(|sr_k|+1)}\)选择第\(i\)个排序规则,然后由所选排序规则生成一个初始序列。在初始序列的基础上,采用RandomLS来改进解。在每次迭代中,它通过从\(R\)中随机选择两个矩形生成一个新的序列\(R'\),并在\(R'\)上调用Heuristic Packing。只有当\(R'\)的解不比\(R\)差时,才用\(R'\)代替\(R\),否则,就放弃\(R'\)。以上的迭代过程重复\(iter\)次。最后,我们更新集合\(sr_k\),以确保它按高度的递减顺序排序,并返回最终找到的最小高度。

基于skyline的best-fit启发式
启发式使用空间来表示放置模式。
给定一个矩形序列\(R\)和容器的宽度\(W_c\),HeuristicPacking将矩形一个接一个地放置。最后返回放置结果的最终高度。在每一步中,它首先从skyline中选择最左下角的线段\(s\),然后使用评分规则选择最适合的矩形,并将选择的矩形放置在\(s\)处,skyline相应地被更新。
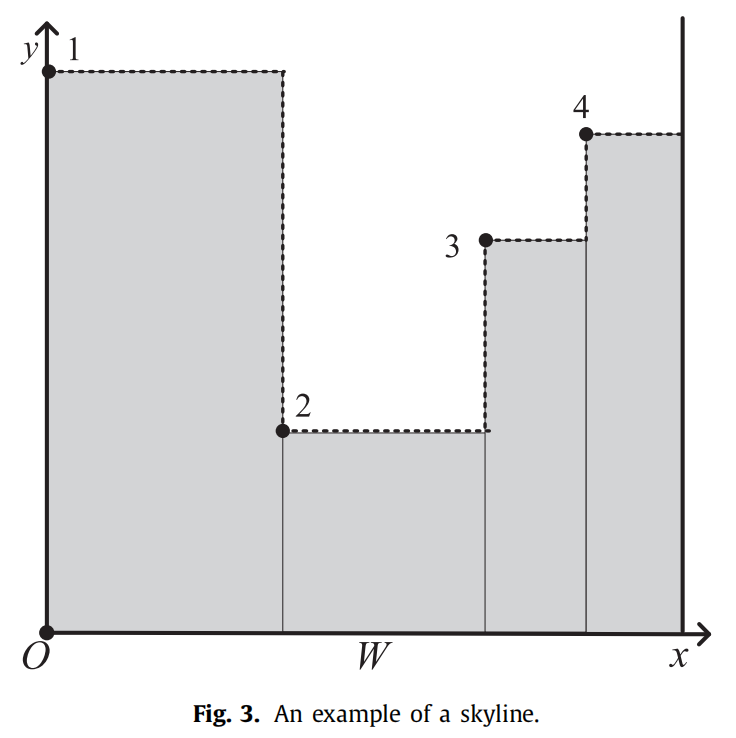
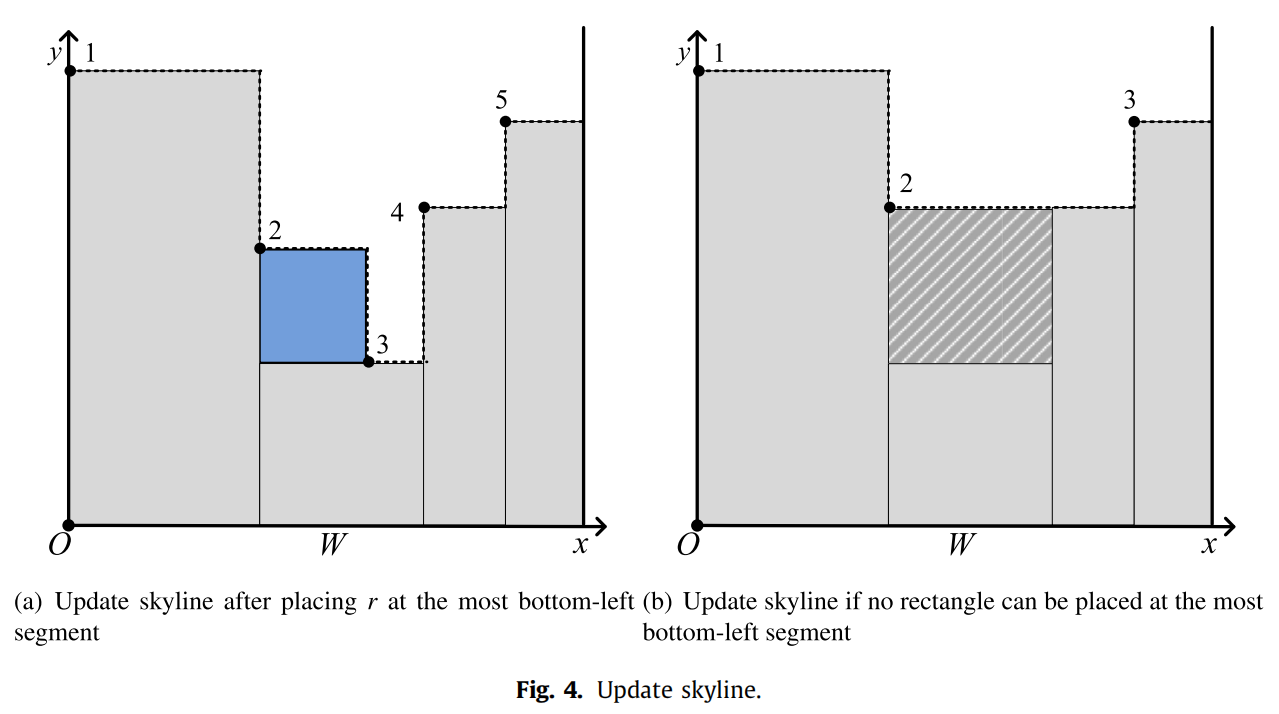
在我们的方法中,当前的填充模式由一条直线的skyline表示,这是一组连续的垂直线段的轮廓线。图3给出了一个天际线的例子,其中每个线段\(s_j\)在其左端点被标记为\(j\)。初始的空放置模式由与容器底部对应的单个线段表示。HeuristicPacking总是选择最左下角的线段\(s\)作为放置矩形的候选段。矩形放置时左下角被放在\(s\)的左点,或者右下角被放在\(s\)的右点。如果有多个矩形可以放置在\(s\)上,它将使用评分规则选择最佳拟合(best-fit)的矩形\(r\)。在将选定的矩形\(r\)放置在\(s\)后,skyline将被更新。添加一个与r的顶边对应的新线段,并更新受影响的现有线段。图4(a)给出了在\(s_2\)处放置一个矩形\(r\)后更新的skyline。如果没有可以放置在\(s\)的矩形,\(s\)将被提高到它较低邻接线段的高度。在图3中,如果在选定的线段\(s_2\)上没有可以放置的矩形,则skyline将被更新,如图4(b)。图4(b)中的阴影区域将被舍弃不再使用。

评分规则
假设当前最左下线段为\(s\),其左(右)竖直的高度为\(h_l\)(\(h_r\)),对于每个矩形适应地放进\(s\)中,如果\(h_l \geq h_r\),可以分类成8种情况(见图5)。如果\(h_l < h_r\)同样也有8种情况。HeuristicPacking选择分数最高的矩形。如果分数一样,选择R中下标靠前的矩形。由于本文中的矩形是可旋转的,对于每个矩形\(r\),尝试将其放在\(s\)时同时放置两个方向,较高的分数定义为\(r\)的分数。